(content inspired from [1])

Motivation

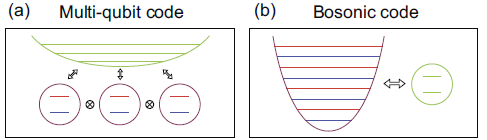
The main idea is to encode the state of a logical qubit across the energy levels of a cavity, which are, in principle, infinite. Conventional quantum error correction codes, such as LDPC or surface codes, use multi-qubit codes to distribute quantum information among multiple qubits. In these codes, harmonic oscillators or resonators typically serve auxiliary roles, such as coupling or readout. In contrast, bosonic codes use the harmonic oscillator itself as the primary medium for storing quantum information, with an ancillary qubit facilitating control and readout, as illustrated in Fig. 1. This approach has the potential to reduce hardware overhead while leveraging the long coherence times characteristic of resonators.

How does it work?

Let error set be \(\epsilon = \{E_i\}\), \(P = \sum_{k} \lvert k\rangle\langle k \rvert\) is the projection operator to the code space, and \(\alpha_{ij}\) is Hermitian matrix.

According to Knill-Laflamme condition, we should have

\begin{equation} P E_i^\dagger E_j P = \alpha_{ij} P, \quad \forall E_i, E_j \in \epsilon \end{equation}

Thus, we can see that

\[\begin{align*} \langle 0_L | E_i^{\dagger} E_j | 0_L \rangle &= \langle 1_L | E_i^{\dagger} E_j | 1_L \rangle = \alpha_{ij}, \\ \langle 0_L | E_i^{\dagger} E_j | 1_L \rangle &= \langle 1_L | E_i^{\dagger} E_j | 0_L \rangle = 0 \end{align*}\]

where \(\lvert 0_L\rangle\) and \(\lvert 1_L\rangle\) are the logical basis states.

For a simple case where \(\epsilon = \{I, a\}\), we must satisfy \(\langle 0_L \lvert a^\dagger a \rvert 0_L \rangle = \langle 1_L \lvert a^\dagger a \rvert 1_L \rangle\).

Bosonic code types

Cat code [2, 3, 4]

This bosonic code is more robust to photon loss errors (Error set = {I, a}). It uses the phase to encode quantum information to the phase (c.f. phase shift key in classical information).

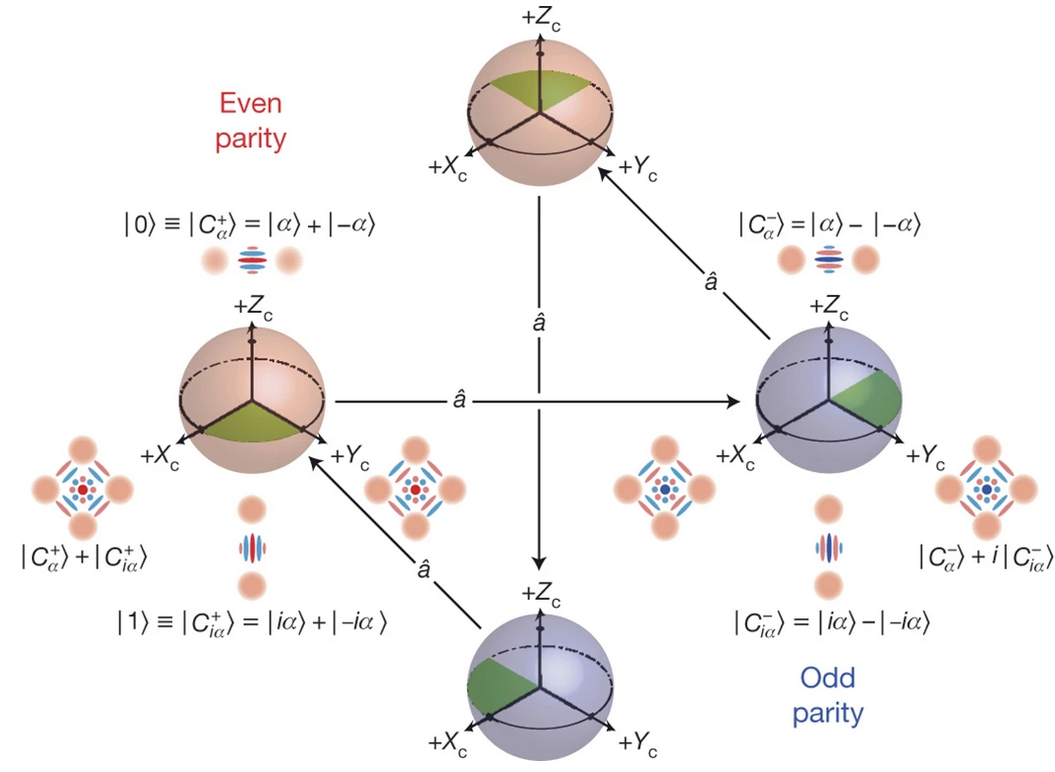
The logical qubit is encoded as: (N is normalization factor)

\[\begin{equation} \begin{split} \lvert 0_L \rangle &= N (\lvert \alpha \rangle + \lvert -\alpha \rangle) \\ \lvert 1_L \rangle &= N (\lvert i \alpha \rangle + \lvert -i \alpha \rangle) \end{split} \end{equation}\]

To orthogonalize both 0 and 1, it is more common to write

\[\begin{align*} \lvert 0_L \rangle &= N (\lvert \alpha \rangle + \lvert -\alpha \rangle + \lvert i \alpha \rangle + \lvert -i \alpha \rangle) \\ \lvert 1_L \rangle &= N (\lvert \alpha \rangle + \lvert - \alpha \rangle - \lvert i \alpha \rangle - \lvert -i\alpha \rangle) \end{align*}\]

The error code is given by

\[\begin{equation} \begin{split} \lvert 0_L \rangle &= N (\lvert \alpha \rangle - \lvert -\alpha \rangle) \\ \lvert 1_L \rangle &= N (\lvert i \alpha \rangle - \lvert -i \alpha \rangle) \end{split} \end{equation}\]

where the coherent state \(\lvert \alpha \rangle = e^{-\frac{\lvert \alpha \rvert^2}{2}} \sum_{n=0}^{\infty} \frac{\alpha^n}{\sqrt{n!}} \lvert n \rangle\).

Binomial code [5, 6]

This correction code is designed to protect from the photon loss error \(a\), photon gain error \(a^\dagger\), and photon dephasing error \(n = a^\dagger a\).

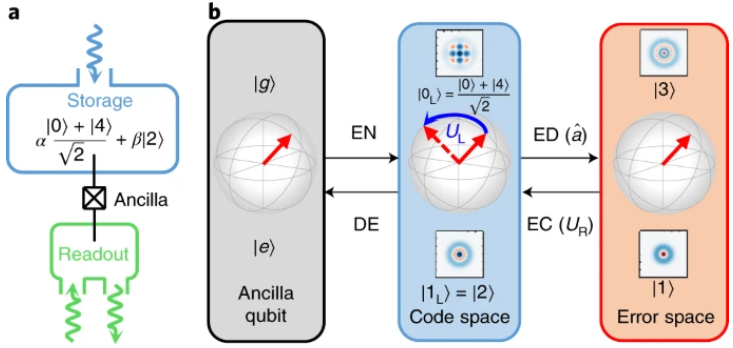
By writing the error set as \(\epsilon = \{I, a, a^2, \ldots a^L, a^\dagger, (a^\dagger)^2, \ldots (a^\dagger)^L, n, n^2, \ldots n^D\}\), the code basis becomes:

\[\begin{equation} \begin{split} |0_L\rangle &= \frac{1}{\sqrt{2^N}} \sum_{\substack{p\ \text{even}}}^{\lfloor 0, N+1 \rfloor} \sqrt{\binom{N+1}{p}}\, \lvert p(S+1) \rangle, \\ |1_L\rangle &= \frac{1}{\sqrt{2^N}} \sum_{\substack{p\ \text{odd}}}^{\lfloor 0, N+1 \rfloor} \sqrt{\binom{N+1}{p}}\, \lvert p(S+1) \rangle. \end{split} \end{equation}\]

where spacing \(S = L+G\), \(N = \max(L, G, 2D)\), \(P\) is from 0 to N+1, and maximum fock number is (N+1)x(S+1).

For the lowest error, the error set is \(\epsilon = \{I, a\}\), giving:

\[\begin{align*} |0_L\rangle &= \frac{1}{\sqrt{2}} (|0\rangle + |4\rangle), \\ |1_L\rangle &= |2\rangle \\ |0_E\rangle &= |3\rangle \\ |1_E\rangle &= |1\rangle \end{align*}\]

Notice that in the logical code, the average n is 2, but in the error code the average n is not equal for 0 and 1, allowing immediate correction.

GKP code [7, 8]

Since \(q = \frac{a+a^\dagger}{2}\) and \(p = \frac{a-a^\dagger}{2i}\), the stabilizers can be written as

\[\begin{equation} \begin{split} S_q &= D(i\sqrt{2\pi}) &= \exp(i 2\sqrt{\pi} q) \\ S_p &= D(\sqrt{2\pi}) &= \exp(-i 2\sqrt{\pi} p) \end{split} \end{equation}\]

We associate Z axis with q, X axis with p, and Y axis with q-p. The Pauli operators are:

\[\begin{equation} \begin{split} X &= D\left(\sqrt{\frac{\pi}{2}}\right) &= \exp(-i \sqrt{\pi} p) \\ Y &= D\left(-\sqrt{\frac{\pi}{2}}(1+i)\right) &= \exp(-i \sqrt{\pi}(p-q)) \\ Z &= D\left(i\sqrt{\frac{\pi}{2}}\right) &= \exp(i \sqrt{\pi} q) \end{split} \end{equation}\]

This can be interpreted as a displacement in phase space. Pauli X causes q-displacement by \(\sqrt{\pi \hbar}\), Pauli Z causes p-displacement by \(\sqrt{\pi \hbar}\), while Hadamard is a rotation by \(\frac{\pi}{2}\).

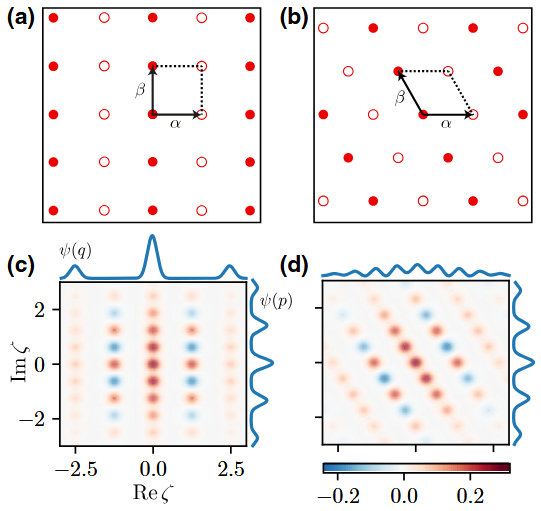
The ideal logical code is given by:

\[\begin{equation} \begin{split} |0_L\rangle &\propto \sum_{k=-\infty}^{\infty} e^{-i n k} \, \lvert 2k \alpha + \beta \rangle, \\ |1_L\rangle &\propto \sum_{k=-\infty}^{\infty} \sum_{l=-\infty}^{\infty} e^{-i n (k+l)/2} \, \lvert (2k+1) \alpha + \beta \rangle. \end{split} \end{equation}\]

where for square lattice, \(\alpha = \sqrt{\frac{\pi}{2}}\) and \(\beta = i \sqrt{\frac{\pi}{2}}\). Accounting to the finite energy effect, the logical code is approximated as \(\lvert \tilde{\mu}_L \rvert \propto e^{-\Delta^2 \hat{a}^\dagger \hat{a}} \lvert \mu_L \rvert\)

References

[1] W Cai et al, Bosonic quantum error correction codes in superconducting quantum circuits, Fundamental Research 2021
[2] Z Leghtas et al, Hardware-Efficient Autonomous Quantum Memory Protection, Physical Review Letters 2013
[3] N Ofek et al, Extending the lifetime of a quantum bit with error correction in superconducting circuits, Nature 2016
[4] H Hutin et al, Preparing Schrödinger Cat States in a Microwave Cavity Using a Neural Network, PRX Quantum 2025
[5] M H Michael et al, New Class of Quantum Error-Correcting Codes for a Bosonic Mode, Physical Review X 2016
[6] L Hu et al, Quantum error correction and universal gate set operation on a binomial bosonic logical qubit, Nature Physics 2019
[7] D Gottesman, A Kitaev, and J Preskill, Encoding a qubit in an oscillator, Physical Review A 2001
[8] A L Grimsmo and S Puri, Quantum Error Correction with the Gottesman-Kitaev-Preskill Code, PRX Quantum 2021